DE MEASURE FASE kan in de green belt worden opgedeeld in twee stappen: Valideren van Data (1), en Huidige Prestatie begrijpen (2). Voor elk van deze stappen zijn verschillende statistische toetsen beschikbaar, afhankelijk van het type data dat in het project gebruikt wordt. Deze worden elk besproken in twee verschillende artikelen: voor discrete data en een apart artikel voor numerieke data.
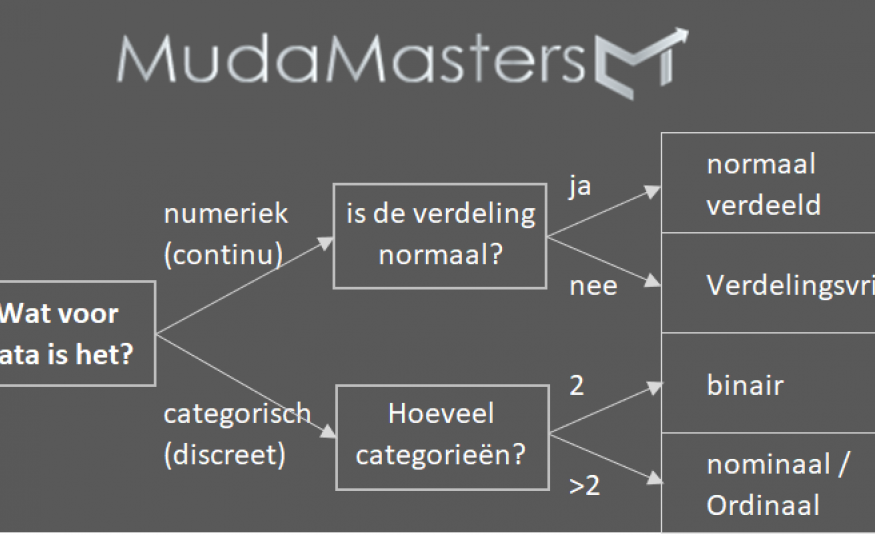
De eerst vraag die we daarom moeten beantwoorden is: wat voor type data hebben wij op dit moment beschikbaar voor ons project? Figuur 2 bevat aan de rechterzijde 4 rijen die elk een type data beschrijven dat beschikbaar is of dat je zou willen verzamelen. Aan de linkerzijde van Figuur 2 staan de vragen die je helpen te bepalen welke rij van figuur 1 je moet zoeken. De eerste vraag beschrijft of de data numeriek of categorisch is, en afhankelijk van dat antwoord kies je de tweede vraag. Bij numerieke data is de tweede vraag of de data normaal verdeeld is of niet, en bij categorische data is de tweede vraag of de dataset binair is. Er ontstaan 4 verschillende datasets.
Figuur 2: vragenschema om “rij” te bepalen in tabel 1
Data type 1 is een numerieke normale verdeling. Dit is een set van data met twee kenmerken: hij is numeriek en de verdeling is normaal. Numeriek betekent dat de data set bestaat uit kwantitatieve data die gemeten wordt in een eenheid en waarmee je kunt rekenen. Uren, temperatuur, centimeters of zelfs IQ punten zijn allen voorbeelden van numerieke data.
Een normale verdeling betekent dat de verdeling symmetrisch geconcentreerd is rond een centrale waarde en afwijkingen van deze centrale waarde steeds onwaarschijnlijker worden naarmate de afwijking groter is. Figuur 3 laat een voorbeeld zien van Math4All, waarbij de intelligentie van mensen wordt weergegeven in een grafiek. Het aantal zeer intelligent hoogbegaafde mensen, zou net zo groot zijn als het aantal geestelijk gehandicapte mensen, maar het veruit meest voorkomende IQ van mensen ligt in het midden. Om te bepalen of jouw data normaal verdeeld is kun je een histogram maken , of een Anderson Darling toets doen om de significantie te berekenen. In een histogram wordt op de Y as geteld hoe vaak een waarde X voorkomt in de reeks. In het voorbeeld hieronder komt dat waarde 100 het meest voor, daarom bevind de piek van de grafiek zich op de waarde 100 op de X-as. Een normale verdeling van intelligentie in dit geval betekent, dat aan beiden kanten van de meest voorkomende waarde 100, de grafiek een gelijke trend laat zien, naar mate we van de 100 afwijken.
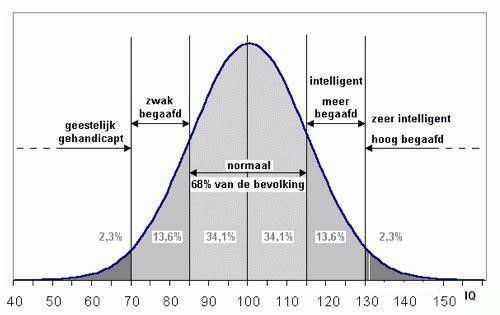
Figuur 3: Intelligentie van mensen als normale verdeling, waarbij een IQ van 100 de meest voorkomende waar is. Bron: http://info.math4all.nl/MathAdore/ha-d35-ap2c.html
Het tweede type data is de verdelingsvrije numerieke data. We spreken hier wederom over kwantitatieve data met waarden die op- en aflopen, maar in dit geval is de data verdelingsvrij, wat betekent dat de afwijkingen niet zo voorspelbaar zijn als bij een normale verdeling. Een voorbeeld hiervan is de leeftijd van mensen (gevonden op de website van de open universiteit), zie figuur 4. Een mediaan leeftijd van 50 jaar ten opzichte van de hoeveelheid nul-jarige zegt in dit geval niets over de hoeveelheid 100 jarige en ook niet over 5-jarige. Bij verdelingsvrije data zou je alle datapunten apart moeten bekijken om een uitspraak over significantie te kunnen doen met elke willekeurige factor. In de rest van de artikelen in deze Green Belt serie laten we de verdelingsvrije data sets buiten de scope en focussen we ons alleen op normaal verdeelde numerieke data.
Figuur 4: verdeling van de leeftijd van Nederlanders in 2006 (BRON: open universiteit)
Het derde type data dat je kan helpen om een statistische toets te kiezen is binaire data. Binaire data is niet numeriek maar categorisch, en bestaat uit twee waarden: ja/nee, man/vrouw, overleefd/overleden. Je kunt niet met deze data rekenen zoals bij numerieke waarden. Je categoriseert de datapunten in twee groepen.
Tot slot zijn er de nominale en ordinale datasets. Ook dit is categorische data, maar dan met meer dan twee categorieën. Ook met deze waarden kun je niet rekenen zoals bij numerieke waarden. Een voorbeeld van nominale waarden zijn telefoonnummers. Een telefoonnummer is een nummer, maar je kan ze niet van elkaar aftrekken. Een tweede voorbeeld is een automerk van de auto van een proefpersoon. Een merk is een verzamelnaam voor een categorie, waarvan er in een dataset snel meer dan 2 zullen voorkomen.
ga verder naar:
Green Belt DMAIC – Introductie van de 8 stappen (binnen 5 fasen)