De standaard deviatie (Sigma, σ voor de populatie, of S voor een sample binnen de populatie) van een data reeks is een meetwaarde die te maken heeft met de spreiding van de nummers in die reeks. Het is een waarde die je verteld hoeveel je gemiddeld genomen van het gemiddelde afwijkt. Hoe kleiner de standaard deviatie – en dus de spreiding -, hoe beter het is.
De standaard deviatie (ook wel de standaardafwijking genoemd) word berekent in 4 stappen:
- Bereken het gemiddelde van de datareeks
- Voor elk nummer in de reeks: trek het gemiddelde van het nummer af, en kwadrateer dat nummer
- Deel de som van alle nummers berekend in stap 2 door het aantal meetwaarden minus 1.
- Neem de wortel van het resultaat uit stap 3.
In formule vorm berekenen we eerst de variatie S2, waarna we de standaard deviatie S berekenen:
Waarin:
S2 = de variatie in de sample,
N = het aantal waardes in de reeks, en
Xi = een van de waarden in de reeks en
µ = het gemiddelde van de reeks.
s = de standaard deviatie = de wortel van s2
Een bloemenvoorbeeld. Stel dat we willen berekenen van de spreiding is van het aantal tulpen in een bos die we op de bloemetjes markt in Amsterdam kunnen kopen. We nemen 10 bossen tulpen ten tellen voor elk van die bossen het aantal tulpen:
9, 2, 5, 4, 12, 7, 8, 11, 9, 3
Stap 1 om de standaard deviatie te bereken is het bepalen van het gemiddelde (µ) van deze reeks:
9+2+5+4+12+7+8+11+9+3/10
= 70/10 = 7
Dus: μ = 7
Stap 2 is om voor elk van de waarden het verschil met het gemiddelde te berekenen en dat cijfer te kwadrateren (zodat het altijd positief uitkomt). Dus:
(9 - 7)2 = (2)2 = 4 (7 - 7)2 = (0)2 = 0
(2 - 7)2 = (-5)2 = 25 (8 - 7)2 = (1)2 = 1
(5 – 7)2 = (-2)2 = 4 (11 - 7)2 = (4)2 = 16
(4 – 7)2 = (-3)2 = 9 (9 - 7)2 = (2)2 = 4
(12 - 7)2 = (5)2 = 25 (3 - 7)2 = (-4)2 = 16
Stap 3 is om als de variantie binnen de reeks tellen we eerst alle waarden van stap 2 bij elkaar op:
4+25+4+9+25+0+1+16+4+16 = 104
En delen dat door het aantal cijfers -1:
104/(10-1) = 104/9 = 11.556
Stap 4, neem de wortel van het antwoorde uit stap 3:
√(11.556) = 3,399
De standaard deviatie van de tulpenbossen is dus 3.399.
Je kunt de berekening uiteraard ook laten uitvoeren in bijvoorbeeld Microsoft Excel, Minitab, JMP of SPSS. Figuur 46 laat de resultaten zien van een gedeelte van de grafische samenvatting van bovenstaand voorbeeld in Minitab. Aan de rechterzijde zien we de waarden mean (gemiddelde) en de StdDev (standaarddeviatie) die overeenkomen met de door ons berekende waarden 7 en 3.399.
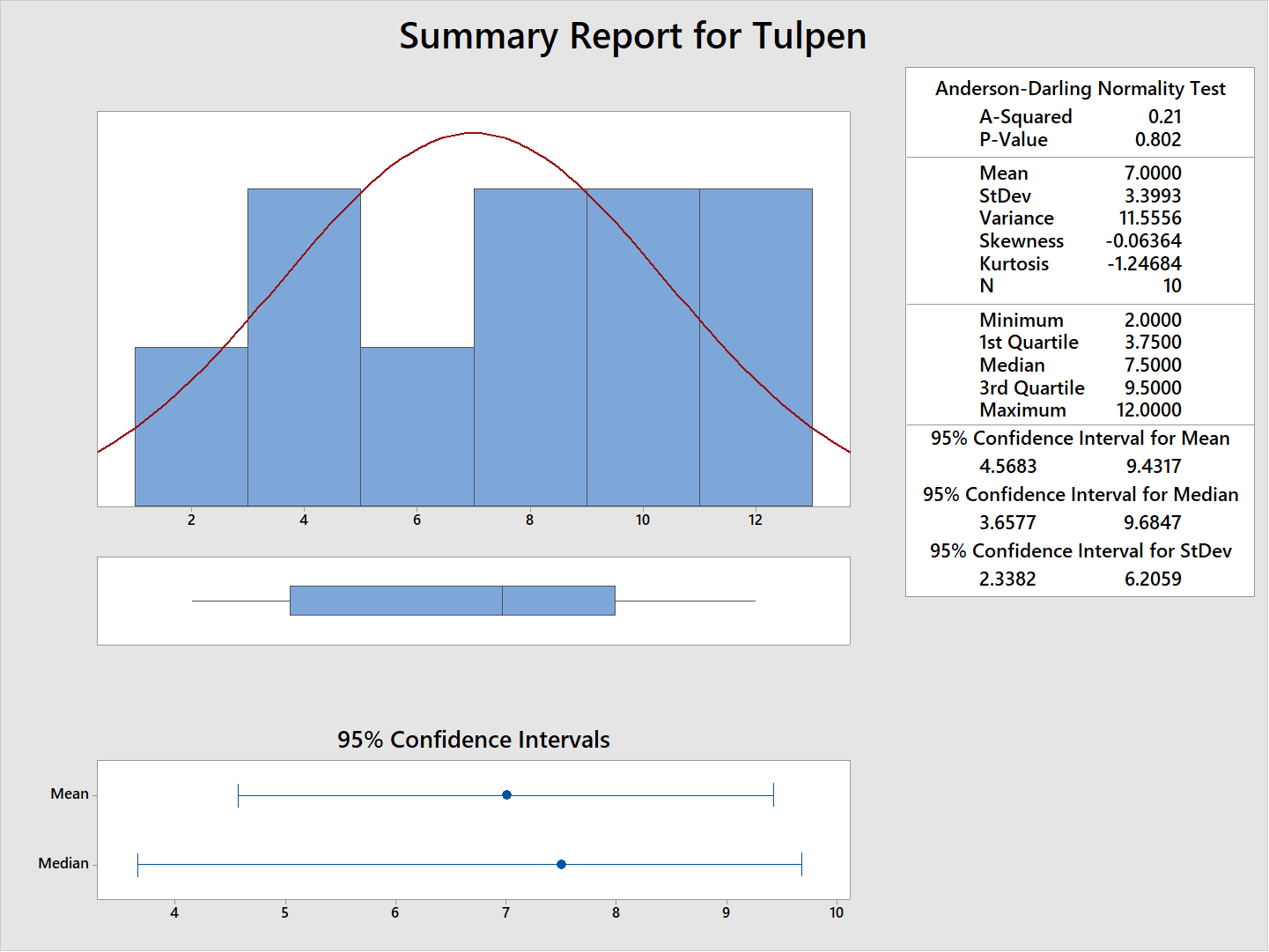
Figuur 58: Standaard deviatie in Tulpen voorbeeld
Ga verder naar:
Introductie in Six Sigma - Wat betekent DMAIC?
* Dit artikel is gekopieerd uit mijn eigen boek: Six Sigma DMAIC - een 8 stappen in 5 Fasen Methode voor jouw Green Belt Project.
BRON:
Panneman, T., Stemann, D., 2021, Six Sigma DMAIC - Een 8 Stappen in 5 Fasen Methode voor jouw Green Belt Project, Dublin: MudaMasters (samenvatting / bestel dit boek)